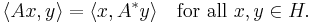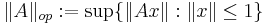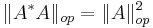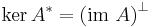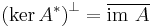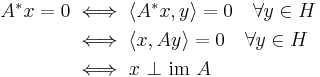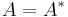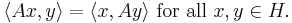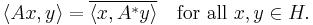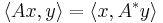Hermitian adjoint

In mathematics, specifically in functional analysis, each linear operator on a Hilbert space has a corresponding adjoint operator. Adjoints of operators generalize conjugate transposes of square matrices to (possibly) infinite-dimensional situations. If one thinks of operators on a Hilbert space as "generalized complex numbers", then the adjoint of an operator plays the role of the complex conjugate of a complex number.

The adjoint of an operator A is also sometimes called the Hermitian conjugate (after Charles Hermite) of A and is denoted by A^* or A^† (the latter especially when used in conjunction with the bra-ket notation).

1 Definition for bounded operators
2 Properties
3 Hermitian operators
4 Adjoints of unbounded operators
5 Adjoints of antilinear operators
6 Other adjoints
7 See also

Definition for bounded operators

Suppose H is a Hilbert space, with inner product 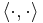$\langle\cdot,\cdot\rangle$ . Consider a continuous linear operator A : H → H (this is the same as a bounded operator).

Using the Riesz representation theorem, one can show that there exists a unique continuous linear operator A* : H → H with the following property:

$\lang Ax , y \rang = \lang x , A^* y \rang \quad \mbox{for all } x,y\in H.$

This operator A* is the adjoint of A. This can be seen as a generalization of the adjoint matrix of a square matrix which has a similar property involving the standard complex inner product.

Properties

Immediate properties:

A** = A
If A is invertible, then so is A*, with (A*)⁻¹ = (A⁻¹)*
(A + B)* = A* + B*
(λA)* = λ* A*, where λ* denotes the complex conjugate of the complex number λ
(AB)* = B*A*

If we define the operator norm of A by

$\| A \| _{op}�:= \sup \{ \|Ax \|�: \| x \| \le 1 \}$

then

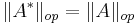$\| A^* \| _{op} = \| A \| _{op}$ .

Moreover,

$\| A^* A \| _{op} = \| A \| _{op}^2$

The set of bounded linear operators on a Hilbert space H together with the adjoint operation and the operator norm form the prototype of a C* algebra.

The relationship between the image of $A$ and the kernel of its adjoint is given by:

$\ker A^* = \left( \operatorname{im}\ A \right)^\bot$

$\left( \ker A^* \right)^\bot = \overline{\operatorname{im}\ A}$

Proof of the first equation:

$\begin{align} A^* x = 0 &\iff \langle A^*x,y \rangle = 0 \quad \forall y \in H \\ &\iff \langle x,Ay \rangle = 0 \quad \forall y \in H \\ &\iff x\ \bot \ \operatorname{im}\ A \end{align}$

The second equation follows from the first by taking the orthogonal space on both sides. Note that in general, the image need not be closed, but the kernel of a continuous operator always is.

Hermitian operators

A bounded operator A : H → H is called Hermitian or self-adjoint if

$A = A^{*}$

which is equivalent to

$\lang Ax , y \rang = \lang x , A y \rang \mbox{ for all } x,y\in H.$

In some sense, these operators play the role of the real numbers (being equal to their own "complex conjugate"). They serve as the model of real-valued observables in quantum mechanics. See the article on self-adjoint operators for a full treatment.

Adjoints of unbounded operators

Many operators of importance are not continuous and are only defined on a subspace of a Hilbert space. In this situation, one may still define an adjoint, as is explained in the articles on self-adjoint operators and unbounded operators.

Adjoints of antilinear operators

For an antilinear operator the definition of adjoint need to be adjusted in order to compensate for the complex conjugation. An adjoint operator of the antilinear operator A on a Hilbert space H is an antilinear operator A* : H → H with the property:

$\lang Ax , y \rang = \overline{\lang x , A^* y \rang} \quad \mbox{for all } x,y\in H.$

Other adjoints

The equation

$\lang Ax , y \rang = \lang x , A^* y \rang$

is formally similar to the defining properties of pairs of adjoint functors in category theory, and this is where adjoint functors got their name from.